A partir de la fecha comenzaremos a publicar un glosario matemático que armamos desde el departamento de Matemática, al cual pueden acceder para consultar alguna definición que no recuerden.
Algoritmo: Método y notación de las distintas formas del cálculo.(1).
Ángulo: Parte del plano determinada por dos semirrectas de origen común.(2)
Ángulo Agudo: Un ángulo es agudo si su amplitud es menor que 90º y mayor que 0°.(2)
Ángulo Recto: Un ángulo es recto si su amplitud es de 90º.(2)
Ángulo Obtuso: Un ángulo es obtuso si su amplitud es mayor que 90º y menor que 180º.(2)
Ángulo Nulo: Un ángulo es nulo si su amplitud es de 0°.(2)
Ángulo Cóncavo: Un ángulo es cóncavo si su amplitud es mayor que 180º y menor que 360º.(2)
Ángulo Convexo: Un ángulo es convexo si su amplitud es menor o igual que 180º y mayor que 0°.(2)
Ángulos Suplementarios: Dos ángulos son suplementarios si sus medidas suman 180º.(2)
Ángulos Complementarios: Dos ángulos son complementarios si sus medidas suman 90º.(2)
Ángulos Adyacentes: Son dos ángulos que tienen el vértice y un lado en común, y los otros dos lados son semirrectas opuestas. Los ángulos adyacentes son suplementarios. (2)
Ángulos consecutivos: dos ángulos son consecutivos cuando tienen el vértice y un lado en común, y los otros dos lados se encuentran en dos semiplanos distintos (respecto del lado común). (2)
Ángulos determinados por dos rectas paralelas cortadas por una tercera: Las rectas a y b dividen el plano en tres zonas: dos exteriores y una interior a las rectas. La transversal divide el plano en dos semiplanos: 1 y 2.(2)
De esta forma quedan determinados 8 ángulos.- Por no estar definida en ese punto
Ángulos Correspondientes: Los ángulos correspondientes se encuentran en el mismo semiplano respecto de la transversal, uno interior y otro exterior. Los ángulos correspondientes entre paralelas son congruentes. (2)
Ángulos Alternos Internos: Los ángulos alternos internos se encuentran en distinto semiplano respecto de la transversal, ambos internos. Los ángulos alternos internos entre paralelas son congruentes. (2)
Ángulos Alternos Externos: los ángulos alternos externos se encuentran en distinto semiplano respecto de la transversal, ambos externos. Los ángulos alternos externos entre paralelas son congruentes. (2)
Ángulos Conjugados Internos: Los ángulos conjugados internos se encuentran en el mismo semiplano respecto de la transversal, ambos internos. Los ángulos conjugados internos entre paralelas son suplementarios. (2)
Ángulos Conjugados Externos: Los ángulos conjugados externos se encuentran en el mismo semiplano respecto de la transversal, ambos externos. Los ángulos conjugados externos entre paralelas son suplementarios. (2)
Ángulos Opuestos por el Vértice: Los ángulos opuestos por el vértice son dos ángulos que tienen el vértice en común y cuyos lados son semirrectas opuestas. Los ángulos opuestos por el vértice son congruentes. (2)
Altura de un Triángulo: La altura de un triángulo es el segmento perpendicular al lado, con un extremo en el vértice opuesto y el otro en el lado, o en su prolongación. Las tres alturas de un triángulo se cortan en un punto. (2)
Bisectriz: La bisectriz es la semirrecta que divide un ángulo en dos ángulos congruentes. (2)
Cateto: Es el nombre de cada uno de los lados opuestos a los ángulos agudos de un triángulo rectángulo. (2)
Cero de una función: Dada una función y = f(x), se llaman ceros de la misma, si es que existen, a los valores que anulan la función. También se les llama raíces de la función. (4)
Complemento: Dado un conjunto A, se llama complemento de A (A elevado a la "c"), respecto del conjunto referencial R, al conjunto formado por los elementos pertenecientes R y no pertenecientes a A. Por ejemplo: si el conjunto referencial es N y A = {naturales pares}, Ac = {naturales impares}. (2)
Concavidad: Una función es cóncava en un determinado punto si la recta tangente en él está por debajo de la gráfica de la función en ese punto. Por ejemplo, esta función es cóncava en "b" y no en "a" (4)
Convexidad: Una función se dice que es convexa en un punto si la gráfica de la función en ese punto está por debajo de la recta tangente a la curva en él. Por ejemplo, en la gráfica anterior es convexa en "a" y no en "b" (4)
Congruentes (en el plano): Se dice de las figuras que al superponerlas coinciden. (2)
Conjunto Definido por Comprensión: Un conjunto se define por comprensión cuando se lo da a conocer por una condición que cumplen todos sus elementos y sólo ellos.
Por ejemplo: B = {x Є N: x ≤ 4}.(2)
Conjunto Definido por Extensión: Un conjunto se define por extensión cuando se lo da a conocer nombrando todos sus elementos.
Por ejemplo: A = {1, 2, 3, 4}. (2)
Derivada Interpretación geométrica: Geométricamente, la derivada de una función en un punto, si existe, representa el valor de la pendiente de la recta tangente a la curva de esa función en ese punto. (4)
Discontinuidad en una función en un punto: Una función puede ser discontinua en un punto si se cumple alguna de las siguientes condiciones:
- f(x) no esta definida en ese punto.
- f(x) no tene límite finito en ese punto.
- f(x) tiene límite finito, pero es distinto al valor que toma la función en ese punto.(4)
Diferencia de Conjuntos: Dados dos conjuntos A y B, A – B es el conjunto cuyos elementos pertenecen a A y no pertenecen a B.
Por ejemplo: si A = {1, 2, 3} y B = {1}, entonces: A – B = {2, 3}.(2)
División: Dados dos números a y b, siendo b ≠ 0, decimos que a ÷ b = c si se cumple que: a = c . b .(2)
División entera: Dados dos números naturales a y b, b ≠ 0, si. a = b . c + r, 0 ≤ r
Divisor: Dados dos números naturales a y b, siendo a distinto de cero, a es divisor de b si es posible expresar el número b como el producto de a por un número natural. Por ejemplo: 8 es el divisor de 40, porque 40 = 8 . 5 (2)
Ecuación: Cualquier condición sobre una o más incognitas que se expresa como una igualdad. Por ejemplo:
- x + 2 = 5 , tiene una solución en el campo de los números naturales (x = 3)
- 3x - 1 = 4 , no tiene solución entera, pero sí racional ( x = 5/3)
- x + y = 10 , tiene infinitos pares de soluciones racionales e irracionales, y finitos pares naturales
- x + 1 = x + 2 , no admite solución en ningún campo numérico
- 2x - 6 = 2(x - 3) , admite infinitas soluciones en cualquier campo numérico
- x al cuadrado - 2 = 0 , tiene dos soluciones dentro del conjunto de los números irracionales.
Ecuación exponencial: Ecuación en la que la incógnita aparece en el exponente de una potencia. Por ejemplo, 2 elevado a la x = 8 es una ecuación exponencial .(4)
Escuadra : Instrumento geométrico con forma de triángulo rectángulo ó compuesto solamente de dos reglas en ángulo recto.(1)
Figura Convexa: Una figura es convexa cuando cualquier par de puntos de la figura determina siempre un segmento incluido en ella. (2)
Figura Cóncava: Una figura es cóncava cuando existe, al menos, un par de puntos pertenecientes a la figura, que determinan un segmento no incluido en ella. (2)
Hipotenusa: Es el lado opuesto al ángulo recto de un triángulo. (2)
Inclusión: Es una relación entre conjuntos. A está incluido en B, si todo elemento de A pertenece a B. Se denota A C B. .
Por ejemplo: A = {2, 3, 4} C {números naturales}. (2)
Intersección: Es una operación entre conjuntos. A ∩ B es el conjunto formado por los elementos que pertenecen a A y a B.
Por ejemplo: A = {a, b, c}, B = {b, c, e}; A ∩ B = {b, c}..(2)
Lugar Geométrico: Es el conjunto de todos los puntos que cumplen cierta condición.
Por ejemplo: el lugar geométrico de todos los puntos del plano que están a una distancia r de un punto fijo O, es la circunferencia de centro O y radio r. .(2)
Mínimo común múltiplo: Es el menor de los múltiplos comunes a varios números.
Módulo de un número real: El módulo o valor absoluto de un número real es la distancia entre ese número y cero. (3)
Múltiplo: Si a y b son números naturales, a es múltiplo de b si a puede escribirse como el producto de b por cualquier otro número natural.
Número primo: Es un número natural mayor que 1, que admite como únicos divisores a 1 y a él mismo
Número irracional: Son aquellos que no pueden ser expresados como cociente o razón de dos números enteros.(3)
Racionalizar: En una fracción algebraica en la que existen raíces en el denominador, convertirla en otra, realizando las operaciones adecuadas, de manera que no quede ninguna raíz en el denominador. (4)
Teorema: Proposición que afirma una verdad demostrable. (1)
FUENTES: El Número que aparece al lado de la definición entre paréntesis.
1-Diccionario Durvan de la lengua española.
2-Patricia Sadovsky, María Pura Melguiso y C.L. Rubinstein de Walkman.
3-Matemática I de Santillana.
4-Diccionario MISMATES (internet).
5-ANAYA, Matemática 1 de M. de Guzmán.
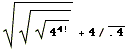
¡Descubrimiento matemático! 26 movimientos son suficientes para resolver el cubo de Rubik en cualquier estado, por muy desordeando que esté. El descubrimiento ha corrido a cargo del profesor de informática Gene Cooperman y el estudiante Dan Kunkle, según cuentan con todos los detalles en 
1.-Realiza estas operaciones:
